Second the reduced form of the recur- rence algorithm is determined. Rahman Ramli Syed Abdul Rahman Al-Haddad Basheera M.
2
Abdulhussain ORCiD Department of Computer and Communication Systems Engineering Universiti Putra Malaysia Selangor Malaysia.
. First sufficient initial values are obtained mathematically. The proposed algorithm makes the computation of the TP superior to that of conventional recurrence algorithms when the polynomial order is large and also accelerates the computational speed of the TPCs. OMs are considered beneficial and effective tools in different digital processing fields.
Finally a new symmetry relation for CHPs is realized. Abdulhussain Abd Rahman Ramli Syed Abdul Rahman Al-Haddad Basheera M. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order Published in IEEE Access in 2017 Web of Science Free Access.
Tchebichef polynomials TPs and their moments are widely used in signal processing due to their remarkable performance in signal analysis feature. In this study a new recurrence algorithm is proposed to generate CHPs for high. On computational aspects of Tchebichef polynomials for higher polynomial order SH Abdulhussain AR Ramli SAR Al-Haddad BM Mahmmod WA Jassim IEEE Access 5.
In the past decades orthogonal moments OMs have received a significant attention and have widely been applied in various applications. Request PDF Stable Computation of Hahn Polynomials for Higher Polynomial Order In this paper we propose a new algorithm for computing Hahn polynomial coefficients HPCs for higher polynomial. Ad Browse Discover Thousands of Science Book Titles for Less.
Abstract Charlier polynomials CHPs and their moments are commonly used in image processing due to their salient performance in the analysis of signals and their capability in signal representation. Discrete Krawtchouk polynomials are widely utilized in different fields for their remarkable characteristics specifically the localization property. On computational aspects of Tchebichef polynomials for higher polynomial order SH Abdulhussain SAR Al-Haddad BM Mahmmod WA Jassim IEEE Access 5 2470-2478 2017.
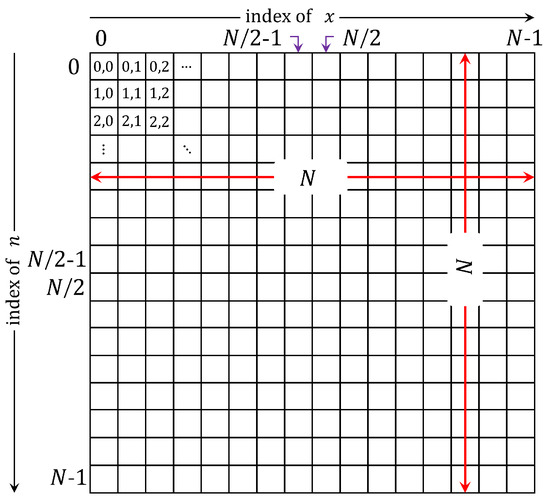
Instability of coefficients for high-order polynomials. The new set of OPs is termed as squared. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order Sadiq H.
On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order. In this paper a new hybrid set of orthogonal polynomials OPs is presented.
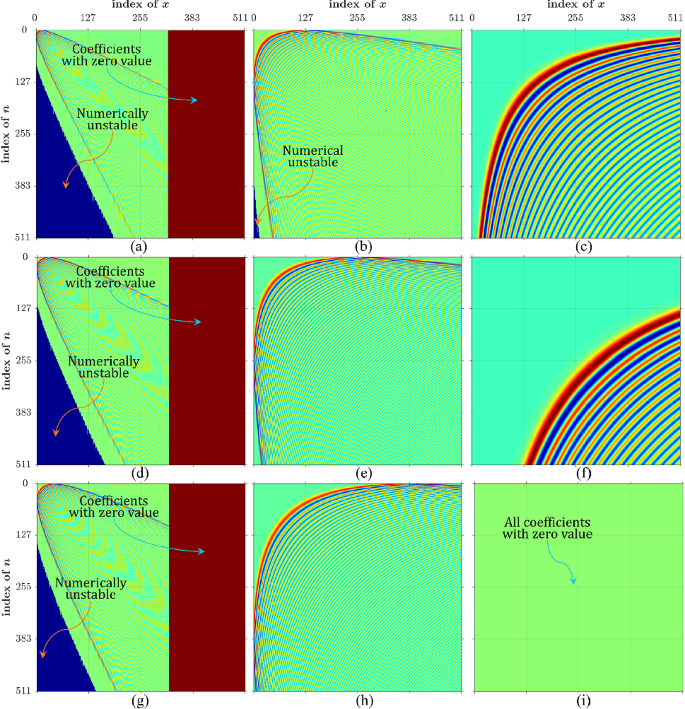
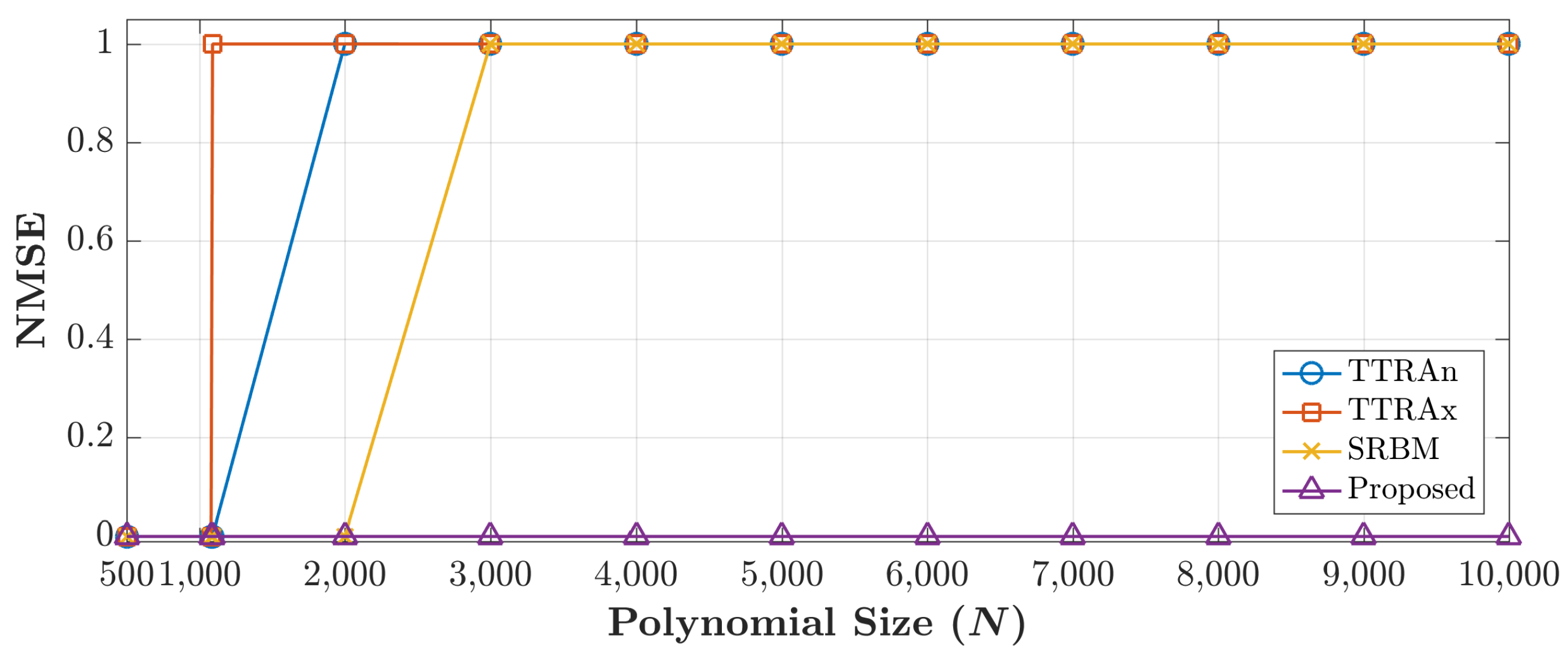
In this study a new recurrence algorithm is proposed to generate CHPs for high-order polynomials. The major issue of CHPs is the numerical instability of coefficients for high-order polynomials. Discrete orthogonal moments are utilized as a feature descriptor for images and video frames in computer vision applications.
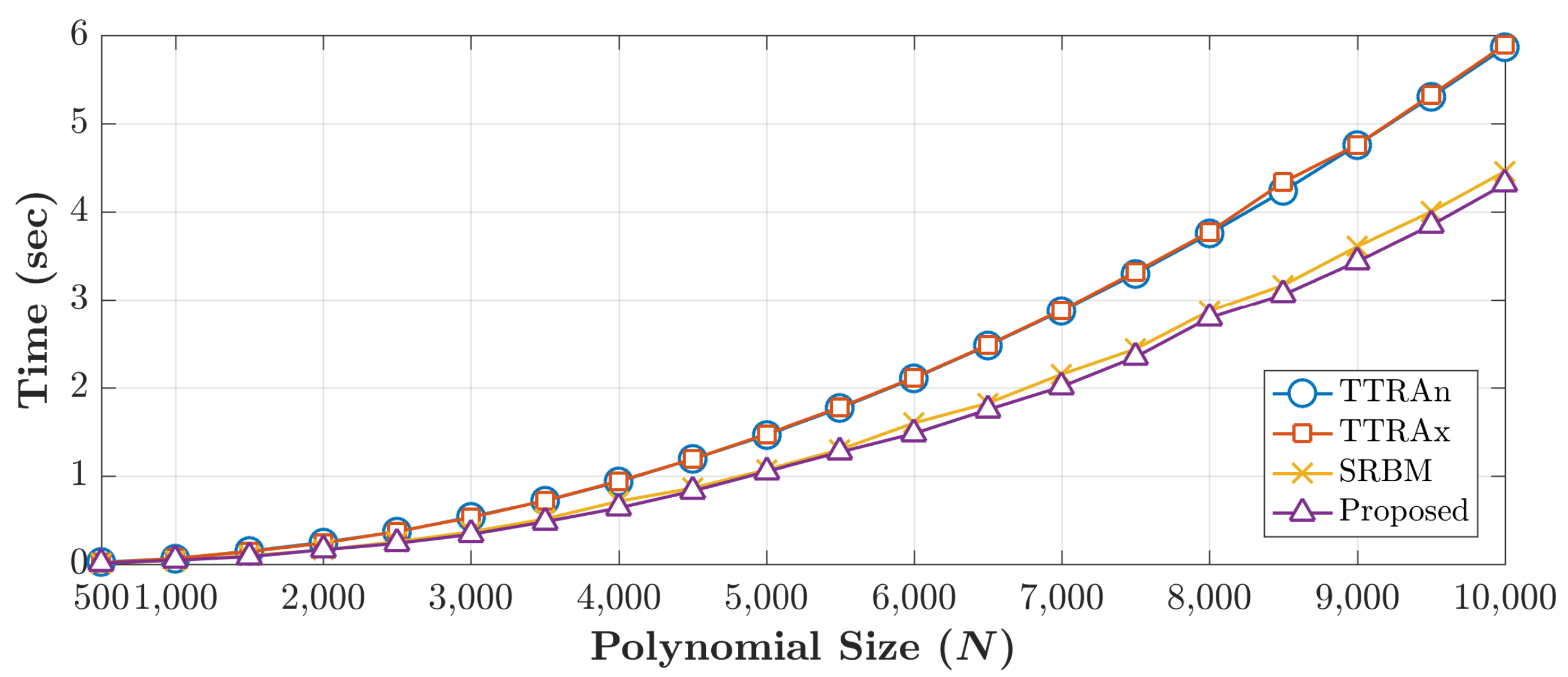
In this paper we present a new method for computing discrete Krawtchouk polynomial coefficients swiftly and.
J Imaging Free Full Text On Computational Aspects Of Krawtchouk Polynomials For High Orders Html
J Imaging Free Full Text On Computational Aspects Of Krawtchouk Polynomials For High Orders Html
2
2
Discrete Chebyshev Polynomials Semantic Scholar
2
2
2
2
2
Discrete Chebyshev Polynomials Semantic Scholar
2
2
2
Fast And Efficient Recursive Algorithm Of Meixner Polynomials Springerlink
2
2
2
J Imaging Free Full Text On Computational Aspects Of Krawtchouk Polynomials For High Orders Html
